BasisSet class tutorial¶
BasisSet class provides a handy abstraction for storing and manipulating orbitals basis sets used in quantum chemistry.
Quick overview¶
The BasisSet requires some basic information
name: name of the basis set as string,element: symbol or name of the element,functions: actual functions in terms of exponents and contraction coeffcients.
Internally the functions attribute is a dictionary with shell labels s, p, d, etc. as keys. A nested dictionary for each shell stores a numpy array array with exponents under key e and a list of contracted functions where each item is a numpy array with a custom dtype storing exponent indices (idx) and contraction
coefficients (cc) of the functions. As an example consider the following structure:
{'s' : {'e' : numpy.array([exp0, exp1, exp2, ...]),
'cf' : [
numpy.array([(i00, c00), (i01, c01), (i02, c02) ...], dtype=[('idx', '<i4'), ('cc', '<f8')]),
numpy.array([(i10, c10), (i11, c11), (i12, c12) ...], dtype=[('idx', '<i4'), ('cc', '<f8')]),
...
]
}
'p' : {'e' : numpy.array([exp0, exp1, exp2, ...]),
'cf' : [
numpy.array([(i00, c00), (i01, c01), (i02, c02) ...], dtype=[('idx', '<i4'), ('cc', '<f8')]),
numpy.array([(i10, c10), (i11, c11), (i12, c12) ...], dtype=[('idx', '<i4'), ('cc', '<f8')]),
...
]
}
...
}
Parsing basis sets¶
At present BasisSet can be created from the following code formats (see below for examples):
The basis sets can e parsed from string or from files. Here only the from_string will be shown but the from_file method has the same call sigantre with first argument being the file name.
However BasisSet can also be serialized into JSON and pickle formats.
cc-pvdz basis for Be in molpro format¶
[1]:
mpstr = '''basis={
!
! BERYLLIUM (9s,4p,1d) -> [3s,2p,1d]
! BERYLLIUM (9s,4p,1d) -> [3s,2p,1d]
s, BE , 2940.0000000, 441.2000000, 100.5000000, 28.4300000, 9.1690000, 3.1960000, 1.1590000, 0.1811000, 0.0589000
c, 1.8, 0.0006800, 0.0052360, 0.0266060, 0.0999930, 0.2697020, 0.4514690, 0.2950740, 0.0125870
c, 1.8, -0.0001230, -0.0009660, -0.0048310, -0.0193140, -0.0532800, -0.1207230, -0.1334350, 0.5307670
c, 9.9, 1
p, BE , 3.6190000, 0.7110000, 0.1951000, 0.0601800
c, 1.3, 0.0291110, 0.1693650, 0.5134580
c, 4.4, 1
d, BE , 0.2380000
c, 1.1, 1
}'''
[2]:
from chemtools.basisset import BasisSet, merge
Construct a BasisSet instance from string
[3]:
pvdz = BasisSet.from_str(mpstr, fmt='molpro', name='cc-pvdz')
[4]:
print(pvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 2940.0000000000 0.00068000 -0.00012300
2 441.2000000000 0.00523600 -0.00096600
3 100.5000000000 0.02660600 -0.00483100
4 28.4300000000 0.09999300 -0.01931400
5 9.1690000000 0.26970200 -0.05328000
6 3.1960000000 0.45146900 -0.12072300
7 1.1590000000 0.29507400 -0.13343500
8 0.1811000000 0.01258700 0.53076700
Uncontracted:
9 0.0589000000 1.00000000
================p shell=================
Contracted:
1 3.6190000000 0.02911100
2 0.7110000000 0.16936500
3 0.1951000000 0.51345800
Uncontracted:
4 0.0601800000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
cc-pvdz basis for Be in Gaussian format¶
[5]:
gaustr = '''****
Be 0
S 8 1.00
2940.0000000 0.0006800
441.2000000 0.0052360
100.5000000 0.0266060
28.4300000 0.0999930
9.1690000 0.2697020
3.1960000 0.4514690
1.1590000 0.2950740
0.1811000 0.0125870
S 8 1.00
2940.0000000 -0.0001230
441.2000000 -0.0009660
100.5000000 -0.0048310
28.4300000 -0.0193140
9.1690000 -0.0532800
3.1960000 -0.1207230
1.1590000 -0.1334350
0.1811000 0.5307670
S 1 1.00
0.0589000 1.0000000
P 3 1.00
3.6190000 0.0291110
0.7110000 0.1693650
0.1951000 0.5134580
P 1 1.00
0.0601800 1.0000000
D 1 1.00
0.2380000 1.0000000
****'''
[6]:
gaupvdz = BasisSet.from_str(gaustr, fmt='gaussian', name='cc-pvdz')
[7]:
print(gaupvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 2940.0000000000 0.00068000 -0.00012300
2 441.2000000000 0.00523600 -0.00096600
3 100.5000000000 0.02660600 -0.00483100
4 28.4300000000 0.09999300 -0.01931400
5 9.1690000000 0.26970200 -0.05328000
6 3.1960000000 0.45146900 -0.12072300
7 1.1590000000 0.29507400 -0.13343500
8 0.1811000000 0.01258700 0.53076700
Uncontracted:
9 0.0589000000 1.00000000
================p shell=================
Contracted:
1 3.6190000000 0.02911100
2 0.7110000000 0.16936500
3 0.1951000000 0.51345800
Uncontracted:
4 0.0601800000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
cc-pvdz for Be in Gamess(US) format¶
[8]:
gamstr = '''$DATA
BERYLLIUM
S 8
1 2940.0000000 0.0006800
2 441.2000000 0.0052360
3 100.5000000 0.0266060
4 28.4300000 0.0999930
5 9.1690000 0.2697020
6 3.1960000 0.4514690
7 1.1590000 0.2950740
8 0.1811000 0.0125870
S 8
1 2940.0000000 -0.0001230
2 441.2000000 -0.0009660
3 100.5000000 -0.0048310
4 28.4300000 -0.0193140
5 9.1690000 -0.0532800
6 3.1960000 -0.1207230
7 1.1590000 -0.1334350
8 0.1811000 0.5307670
S 1
1 0.0589000 1.0000000
P 3
1 3.6190000 0.0291110
2 0.7110000 0.1693650
3 0.1951000 0.5134580
P 1
1 0.0601800 1.0000000
D 1
1 0.2380000 1.0000000
$END
'''
[9]:
gampvdz = BasisSet.from_str(gamstr, fmt='gamessus', name='cc-pvdz')
[10]:
print(gampvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 2940.0000000000 0.00068000 -0.00012300
2 441.2000000000 0.00523600 -0.00096600
3 100.5000000000 0.02660600 -0.00483100
4 28.4300000000 0.09999300 -0.01931400
5 9.1690000000 0.26970200 -0.05328000
6 3.1960000000 0.45146900 -0.12072300
7 1.1590000000 0.29507400 -0.13343500
8 0.1811000000 0.01258700 0.53076700
Uncontracted:
9 0.0589000000 1.00000000
================p shell=================
Contracted:
1 3.6190000000 0.02911100
2 0.7110000000 0.16936500
3 0.1951000000 0.51345800
Uncontracted:
4 0.0601800000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
Basis sets for multiple elements¶
If basis sets for multiple elements are given in the format compatible with EMSL BSE the parser returns a dictionary with element symbols as keys and BasisSet objects as values. For example below is the cc-pCVDZ basis set string in molpro format for Be, Mg, Ca as downloaded from EMSL. Remaining Gamess(US) and Gaussian formats can be parsed analogously.
[11]:
multi = '''
basis={
!
! BERYLLIUM (10s,5p,1d) -> [4s,3p,1d]
! BERYLLIUM (9s,4p,1d) -> [3s,2p,1d]
! BERYLLIUM (1s,1p)
s, BE , 2940.0000000, 441.2000000, 100.5000000, 28.4300000, 9.1690000, 3.1960000, 1.1590000, 0.1811000, 0.0589000, 1.8600000
c, 1.8, 0.0006800, 0.0052360, 0.0266060, 0.0999930, 0.2697020, 0.4514690, 0.2950740, 0.0125870
c, 1.8, -0.0001230, -0.0009660, -0.0048310, -0.0193140, -0.0532800, -0.1207230, -0.1334350, 0.5307670
c, 9.9, 1
c, 10.10, 1
p, BE , 3.6190000, 0.7110000, 0.1951000, 0.0601800, 6.1630000
c, 1.3, 0.0291110, 0.1693650, 0.5134580
c, 4.4, 1
c, 5.5, 1
d, BE , 0.2380000
c, 1.1, 1
! MAGNESIUM (13s,9p,2d) -> [5s,4p,2d]
! MAGNESIUM (12s,8p,1d) -> [4s,3p,1d]
! MAGNESIUM (1s,1p,1d)
s, MG , 47390.0000000, 7108.0000000, 1618.0000000, 458.4000000, 149.3000000, 53.5900000, 20.7000000, 8.3840000, 2.5420000, 0.8787000, 0.1077000, 0.0399900, 3.4220000
c, 1.11, 0.346023D-03, 0.268077D-02, 0.138367D-01, 0.551767D-01, 0.169660D+00, 0.364703D+00, 0.406856D+00, 0.135089D+00, 0.490884D-02, 0.286460D-03, 0.264590D-04
c, 1.11, -0.877839D-04, -0.674725D-03, -0.355603D-02, -0.142154D-01, -0.476748D-01, -0.114892D+00, -0.200676D+00, -0.341224D-01, 0.570454D+00, 0.542309D+00, 0.218128D-01
c, 1.11, 0.169628D-04, 0.129865D-03, 0.688831D-03, 0.273533D-02, 0.931224D-02, 0.223265D-01, 0.411195D-01, 0.545642D-02, -0.134012D+00, -0.256176D+00, 0.605856D+00
c, 12.12, 1
c, 13.13, 1
p, MG , 179.9000000, 42.1400000, 13.1300000, 4.6280000, 1.6700000, 0.5857000, 0.1311000, 0.0411200, 8.2790000
c, 1.7, 0.538161D-02, 0.392418D-01, 0.157445D+00, 0.358535D+00, 0.457226D+00, 0.215918D+00, 0.664948D-02
c, 1.7, -0.865948D-03, -0.615978D-02, -0.261519D-01, -0.570647D-01, -0.873906D-01, -0.122990D-01, 0.502085D+00
c, 8.8, 1
c, 9.9, 1
d, MG , 0.1870000, 3.7040000
c, 1.1, 1
c, 2.2, 1
! CALCIUM (15s,12p,6d) -> [6s,5p,3d]
! CALCIUM (14s,11p,5d) -> [5s,4p,2d]
! CALCIUM (1s,1p,1d)
s, CA , 190000.7000000, 28481.4600000, 6482.7010000, 1835.8910000, 598.7243000, 215.8841000, 84.0124200, 34.2248800, 10.0249700, 4.0559200, 1.0202610, 0.4268650, 0.0633470, 0.0263010, 1.1143000
c, 1.13, 0.00022145, 0.00171830, 0.00892348, 0.03630183, 0.11762223, 0.28604352, 0.42260708, 0.25774366, 0.02391893, -0.00495218, 0.00171779, -0.00089209, 0.00024510
c, 1.13, -0.00006453, -0.00049662, -0.00262826, -0.01066845, -0.03713509, -0.09804284, -0.20342692, -0.15244655, 0.48279406, 0.62923839, 0.06164842, -0.01479971, 0.00361089
c, 1.13, 0.00002223, 0.00017170, 0.00090452, 0.00370343, 0.01283750, 0.03475459, 0.07303491, 0.06100083, -0.24292928, -0.48708500, 0.56502804, 0.65574386, 0.02672894
c, 1.13, 0.00000531, 0.00004111, 0.00021568, 0.00088827, 0.00305813, 0.00837608, 0.01741056, 0.01515453, -0.06207919, -0.12611803, 0.17360694, 0.37822943, -0.65964698
c, 14.14, 1
c, 15.15, 1
p, CA , 1072.0430000, 253.8439000, 81.3162600, 30.2418300, 12.1011000, 5.0225540, 1.9092200, 0.7713040, 0.3005700, 0.0766490, 0.0277720, 1.5101000
c, 1.10, 0.00198166, 0.01612944, 0.07657851, 0.23269594, 0.42445210, 0.37326402, 0.07868530, -0.00599927, 0.00264257, -0.00085694
c, 1.10, -0.00064891, -0.00527907, -0.02581131, -0.08062892, -0.15846552, -0.12816816, 0.25610103, 0.58724068, 0.30372561, 0.01416451
c, 1.10, 0.00013595, 0.00109420, 0.00542680, 0.01674718, 0.03389863, 0.02531183, -0.05895713, -0.15876120, -0.08554523, 0.54464665
c, 11.11, 1
c, 12.12, 1
d, CA , 10.3182000, 2.5924200, 0.7617000, 0.2083800, 0.0537000, 1.3743000
c, 1.4, 0.03284900, 0.14819200, 0.31092100, 0.45219500
c, 5.5, 1
c, 6.6, 1
}'''
It can be parsed analogously to a basis for single element using from_string method or from_file when the basis is stored in a text file
[12]:
bsdict = BasisSet.from_str(multi, name='cc-pCVDZ', fmt='molpro')
The parsed basis set can be accessed by element symbols
[13]:
bsdict.keys()
[13]:
dict_keys(['Be', 'Mg', 'Ca'])
To test the parsed basis we can print some of the properties of the basis sets
[14]:
for symbol, bs in bsdict.items():
print(symbol, bs.name, bs.element, bs.contraction_scheme())
Be cc-pCVDZ Be (10s5p1d) -> [4s3p1d] : {8 8 1 1/3 1 1/1}
Mg cc-pCVDZ Mg (13s9p2d) -> [5s4p2d] : {11 11 11 1 1/7 7 1 1/1 1}
Ca cc-pCVDZ Ca (15s12p6d) -> [6s5p3d] : {13 13 13 13 1 1/10 10 10 1 1/4 1 1}
Initialization of BasisSet from various sequences¶
The BasisSet exponents can be generated from following sequences:
even tempered
well tempered
legendre expansion
To generate the exponents from_sequence classmethod is used. The arguments that have to be specified are
formuladescribing the sequence, one of eventemp, welltemp, legendre, can be a single value or a list of values with the same length asfunsnameof the basis setelementfunsa list of 4-tuples, where the tuple elements are shell, sequence name, number of functions, parameters
even tempered¶
10 s functions with \(\alpha=0.5\) and \(\beta=2.0\)
[15]:
et = BasisSet.from_sequence(name='my basis', element='Be', funs=[('s', 'et', 10, (0.5, 2.0))])
print(et)
Name = my basis
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Uncontracted:
1 256.0000000000 1.00000000
2 128.0000000000 1.00000000
3 64.0000000000 1.00000000
4 32.0000000000 1.00000000
5 16.0000000000 1.00000000
6 8.0000000000 1.00000000
7 4.0000000000 1.00000000
8 2.0000000000 1.00000000
9 1.0000000000 1.00000000
10 0.5000000000 1.00000000
8 s functions with \(\alpha=0.8\), \(\beta=2.5\) and 6 p functions with \(\alpha=0.2\), \(\beta=3.0\)
[16]:
et2 = BasisSet.from_sequence(name='my basis', element='Be',
funs=[('s', 'et', 8, (0.8, 2.5)), ('p', 'et', 6, (0.2, 3.0))])
print(et)
Name = my basis
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Uncontracted:
1 256.0000000000 1.00000000
2 128.0000000000 1.00000000
3 64.0000000000 1.00000000
4 32.0000000000 1.00000000
5 16.0000000000 1.00000000
6 8.0000000000 1.00000000
7 4.0000000000 1.00000000
8 2.0000000000 1.00000000
9 1.0000000000 1.00000000
10 0.5000000000 1.00000000
well tempered¶
[17]:
wt = BasisSet.from_sequence(name='my basis', element='Be', funs=[('p', 'wt', 6, (0.5, 2.0, 0.9, 1.2))])
print(wt)
Name = my basis
Element = Be
Family = None
Kind = None
Functions:
================p shell=================
Uncontracted:
1 30.4000000000 1.00000000
2 13.7851550240 1.00000000
3 6.2130589876 1.00000000
4 2.7834955070 1.00000000
5 1.2408224685 1.00000000
6 0.5524120339 1.00000000
legendre¶
[18]:
leg = BasisSet.from_sequence(name='my basis', element='Be', funs=[('d', 'le', 8, (0.5, 2.0))])
print(leg)
Name = my basis
Element = Be
Family = None
Kind = None
Functions:
================d shell=================
Uncontracted:
1 12.1824939607 1.00000000
2 6.8796751109 1.00000000
3 3.8850772086 1.00000000
4 2.1939735051 1.00000000
5 1.2389765975 1.00000000
6 0.6996725374 1.00000000
7 0.3951177613 1.00000000
8 0.2231301601 1.00000000
direct specification of exponents¶
[19]:
de = BasisSet.from_sequence(name='my exponents', element='Be', funs=[('s', 'exp', 5, (0.01, 0.1, 0.5, 2.0, 10.0))])
print(de)
Name = my exponents
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Uncontracted:
1 10.0000000000 1.00000000
2 2.0000000000 1.00000000
3 0.5000000000 1.00000000
4 0.1000000000 1.00000000
5 0.0100000000 1.00000000
mixed¶
In this example a basis set is created by taking:
6 s functions generated from an even tempered sequence
4 p functions generated from a well tempered sequence
4 d functions generated from a legendre sequence
[20]:
basis = BasisSet.from_sequence(name='composite', element='He',
funs=[('s', 'et', 6, (0.5, 4.0)),
('p', 'wt', 4, (0.9, 3.0, 0.8, 1.2)),
('d', 'le', 4, (1.0, 2.5))])
print(basis)
Name = composite
Element = He
Family = None
Kind = None
Functions:
================s shell=================
Uncontracted:
1 512.0000000000 1.00000000
2 128.0000000000 1.00000000
3 32.0000000000 1.00000000
4 8.0000000000 1.00000000
5 2.0000000000 1.00000000
6 0.5000000000 1.00000000
================p shell=================
Uncontracted:
1 43.7400000000 1.00000000
2 12.6882653049 1.00000000
3 3.6401946084 1.00000000
4 1.0364144910 1.00000000
================d shell=================
Uncontracted:
1 33.1154519587 1.00000000
2 6.2547009519 1.00000000
3 1.1813604129 1.00000000
4 0.2231301601 1.00000000
Conversion to formats of different quantum chemistry programs¶
The following basis set formats are supported:
In addition a converter to LaTeX is also available.
If you would like some other formats to be included please consider submitting an issue describing the request.
Gaussian format¶
[21]:
print(pvdz.to_gaussian())
****
Be 0
S 8 1.00
2940.0000000000 0.00068000
441.2000000000 0.00523600
100.5000000000 0.02660600
28.4300000000 0.09999300
9.1690000000 0.26970200
3.1960000000 0.45146900
1.1590000000 0.29507400
0.1811000000 0.01258700
S 8 1.00
2940.0000000000 -0.00012300
441.2000000000 -0.00096600
100.5000000000 -0.00483100
28.4300000000 -0.01931400
9.1690000000 -0.05328000
3.1960000000 -0.12072300
1.1590000000 -0.13343500
0.1811000000 0.53076700
S 1 1.00
0.0589000000 1.00000000
P 3 1.00
3.6190000000 0.02911100
0.7110000000 0.16936500
0.1951000000 0.51345800
P 1 1.00
0.0601800000 1.00000000
D 1 1.00
0.2380000000 1.00000000
****
NwChem format¶
[22]:
print(pvdz.to_nwchem())
BASIS "ao basis" PRINT
Be s
2940.0000000000 0.00068000 -0.00012300
441.2000000000 0.00523600 -0.00096600
100.5000000000 0.02660600 -0.00483100
28.4300000000 0.09999300 -0.01931400
9.1690000000 0.26970200 -0.05328000
3.1960000000 0.45146900 -0.12072300
1.1590000000 0.29507400 -0.13343500
0.1811000000 0.01258700 0.53076700
Be s
0.0589000000 1.00000000
Be p
3.6190000000 0.02911100
0.7110000000 0.16936500
0.1951000000 0.51345800
Be p
0.0601800000 1.00000000
Be d
0.2380000000 1.00000000
END
Cfour/AcesII format¶
[23]:
print(pvdz.to_cfour(comment="my comment"))
Be:cc-pvdz
my comment
3
0 1 2
3 2 1
9 4 1
2940.00000000 441.20000000 100.50000000 28.43000000 9.16900000
3.19600000 1.15900000 0.18110000 0.05890000
0.00068000 -0.00012300 0.00000000
0.00523600 -0.00096600 0.00000000
0.02660600 -0.00483100 0.00000000
0.09999300 -0.01931400 0.00000000
0.26970200 -0.05328000 0.00000000
0.45146900 -0.12072300 0.00000000
0.29507400 -0.13343500 0.00000000
0.01258700 0.53076700 0.00000000
0.00000000 0.00000000 1.00000000
3.61900000 0.71100000 0.19510000 0.06018000
0.02911100 0.00000000
0.16936500 0.00000000
0.51345800 0.00000000
0.00000000 1.00000000
0.23800000
1.00000000
Dalton format¶
[24]:
print(pvdz.to_dalton())
! cc-pvdz
! s functions
H 9 3
2940.0000000000 0.0006800000 -0.0001230000 0.0000000000
441.2000000000 0.0052360000 -0.0009660000 0.0000000000
100.5000000000 0.0266060000 -0.0048310000 0.0000000000
28.4300000000 0.0999930000 -0.0193140000 0.0000000000
9.1690000000 0.2697020000 -0.0532800000 0.0000000000
3.1960000000 0.4514690000 -0.1207230000 0.0000000000
1.1590000000 0.2950740000 -0.1334350000 0.0000000000
0.1811000000 0.0125870000 0.5307670000 0.0000000000
0.0589000000 0.0000000000 0.0000000000 1.0000000000
! p functions
H 4 2
3.6190000000 0.0291110000 0.0000000000
0.7110000000 0.1693650000 0.0000000000
0.1951000000 0.5134580000 0.0000000000
0.0601800000 0.0000000000 1.0000000000
! d functions
H 1 1
0.2380000000 1.0000000000
Gamess(US) format¶
[25]:
print(pvdz.to_gamessus())
S 8
1 2940.0000000000 0.00068000
2 441.2000000000 0.00523600
3 100.5000000000 0.02660600
4 28.4300000000 0.09999300
5 9.1690000000 0.26970200
6 3.1960000000 0.45146900
7 1.1590000000 0.29507400
8 0.1811000000 0.01258700
S 8
1 2940.0000000000 -0.00012300
2 441.2000000000 -0.00096600
3 100.5000000000 -0.00483100
4 28.4300000000 -0.01931400
5 9.1690000000 -0.05328000
6 3.1960000000 -0.12072300
7 1.1590000000 -0.13343500
8 0.1811000000 0.53076700
S 1
1 0.0589000000 1.00000000
P 3
1 3.6190000000 0.02911100
2 0.7110000000 0.16936500
3 0.1951000000 0.51345800
P 1
1 0.0601800000 1.00000000
D 1
1 0.2380000000 1.00000000
Molpro format¶
[26]:
print(pvdz.to_molpro(withpars=True))
basis={
s, Be, 2940.0000000000, 441.2000000000, 100.5000000000, 28.4300000000, 9.1690000000, 3.1960000000, 1.1590000000, 0.1811000000, 0.0589000000
c, 1.8, 0.00068000, 0.00523600, 0.02660600, 0.09999300, 0.26970200, 0.45146900, 0.29507400, 0.01258700
c, 1.8, -0.00012300, -0.00096600, -0.00483100, -0.01931400, -0.05328000, -0.12072300, -0.13343500, 0.53076700
c, 9.9, 1.00000000
p, Be, 3.6190000000, 0.7110000000, 0.1951000000, 0.0601800000
c, 1.3, 0.02911100, 0.16936500, 0.51345800
c, 4.4, 1.00000000
d, Be, 0.2380000000
c, 1.1, 1.00000000
}
LaTeX format¶
[27]:
print(pvdz.to_latex())
\begin{tabular}{rrrr}
No. & \multicolumn{1}{c}{Exponent} & \multicolumn{2}{c}{Coefficients } \\
\hline
\multicolumn{4}{c}{ s shell } \\ \hline
1 & 2940.0000000000 & 0.00068000 & -0.00012300 \\
2 & 441.2000000000 & 0.00523600 & -0.00096600 \\
3 & 100.5000000000 & 0.02660600 & -0.00483100 \\
4 & 28.4300000000 & 0.09999300 & -0.01931400 \\
5 & 9.1690000000 & 0.26970200 & -0.05328000 \\
6 & 3.1960000000 & 0.45146900 & -0.12072300 \\
7 & 1.1590000000 & 0.29507400 & -0.13343500 \\
8 & 0.1811000000 & 0.01258700 & 0.53076700 \\
9 & 0.0589000000 & \\
\hline
\multicolumn{4}{c}{ p shell } \\ \hline
1 & 3.6190000000 & 0.02911100 \\
2 & 0.7110000000 & 0.16936500 \\
3 & 0.1951000000 & 0.51345800 \\
4 & 0.0601800000 & \\
\hline
\multicolumn{4}{c}{ d shell } \\ \hline
1 & 0.2380000000 & \\
\end{tabular}
Useful tools for working with BasisSet¶
Attributes¶
[28]:
pvdz.name
[28]:
'cc-pvdz'
[29]:
pvdz.element
[29]:
'Be'
Inspection methods describing the BasisSet¶
[30]:
pvdz.contraction_scheme()
[30]:
'(9s4p1d) -> [3s2p1d] : {8 8 1/3 1/1}'
[31]:
pvdz.contraction_type()
[31]:
'unknown'
Number of contracted functions per shell
[32]:
pvdz.contractions_per_shell()
[32]:
[3, 2, 1]
Contraction matrix for a given shell, where rows numbers correspond to the exponent indices and column contain the conntraction coefficients for each function.
[33]:
pvdz.contraction_matrix('s')
[33]:
array([[ 6.80000000e-04, -1.23000000e-04, 0.00000000e+00],
[ 5.23600000e-03, -9.66000000e-04, 0.00000000e+00],
[ 2.66060000e-02, -4.83100000e-03, 0.00000000e+00],
[ 9.99930000e-02, -1.93140000e-02, 0.00000000e+00],
[ 2.69702000e-01, -5.32800000e-02, 0.00000000e+00],
[ 4.51469000e-01, -1.20723000e-01, 0.00000000e+00],
[ 2.95074000e-01, -1.33435000e-01, 0.00000000e+00],
[ 1.25870000e-02, 5.30767000e-01, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
[34]:
pvdz.contraction_matrix('p')
[34]:
array([[ 0.029111, 0. ],
[ 0.169365, 0. ],
[ 0.513458, 0. ],
[ 0. , 1. ]])
Calculate the total number of functions in the basis set. By default the number is calculated assuming spherical harmonics, namely 5d functions, 7f functions, etc.
[35]:
pvdz.nf()
[35]:
14
The number of functions assuming cartesian gaussians, namely 6d components, 10f components, etc., can be calcualted by passing spherical=False argument.
[36]:
pvdz.nf(spherical=False)
[36]:
15
Calculate the number of primitive functions assuming sphrical or cartesian gaussians.
[37]:
pvdz.nprimitive()
[37]:
26
[38]:
pvdz.nprimitive(spherical=False)
[38]:
27
[39]:
pvdz.primitives_per_shell()
[39]:
[9, 4, 1]
[40]:
pvdz.primitives_per_contraction()
[40]:
[[8, 8, 1], [3, 1], [1]]
If you want to extract just the exponents you can use the get_exponents method, that by default returns a dict of exponents in each shell.
[41]:
pvdz.get_exponents()
[41]:
{'d': array([ 0.238]),
'p': array([ 3.619 , 0.711 , 0.1951 , 0.06018]),
's': array([ 2.94000000e+03, 4.41200000e+02, 1.00500000e+02,
2.84300000e+01, 9.16900000e+00, 3.19600000e+00,
1.15900000e+00, 1.81100000e-01, 5.89000000e-02])}
If you want all exponents in one array pass the asdict=False argument
[42]:
pvdz.get_exponents(asdict=False)
[42]:
array([ 2.94000000e+03, 4.41200000e+02, 1.00500000e+02,
2.84300000e+01, 9.16900000e+00, 3.61900000e+00,
3.19600000e+00, 1.15900000e+00, 7.11000000e-01,
2.38000000e-01, 1.95100000e-01, 1.81100000e-01,
6.01800000e-02, 5.89000000e-02])
Sorting¶
Each shell of the BasisSet can be sorted with respect to the exponents, the default order is descending
[43]:
pvdz.sort()
print(pvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 2940.0000000000 0.00068000 -0.00012300
2 441.2000000000 0.00523600 -0.00096600
3 100.5000000000 0.02660600 -0.00483100
4 28.4300000000 0.09999300 -0.01931400
5 9.1690000000 0.26970200 -0.05328000
6 3.1960000000 0.45146900 -0.12072300
7 1.1590000000 0.29507400 -0.13343500
8 0.1811000000 0.01258700 0.53076700
Uncontracted:
9 0.0589000000 1.00000000
================p shell=================
Contracted:
1 3.6190000000 0.02911100
2 0.7110000000 0.16936500
3 0.1951000000 0.51345800
Uncontracted:
4 0.0601800000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
the basis set was already sorted so there is no difference but we can also sort in ascending order to see the result
[44]:
pvdz.sort(reverse=True)
print(pvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 0.1811000000 0.01258700 0.53076700
2 1.1590000000 0.29507400 -0.13343500
3 3.1960000000 0.45146900 -0.12072300
4 9.1690000000 0.26970200 -0.05328000
5 28.4300000000 0.09999300 -0.01931400
6 100.5000000000 0.02660600 -0.00483100
7 441.2000000000 0.00523600 -0.00096600
8 2940.0000000000 0.00068000 -0.00012300
Uncontracted:
9 0.0589000000 1.00000000
================p shell=================
Contracted:
1 0.1951000000 0.51345800
2 0.7110000000 0.16936500
3 3.6190000000 0.02911100
Uncontracted:
4 0.0601800000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
Normalization of the contraction coefficients¶
To check if the contraction coefficients for each function are properly normalized to unity the normalized method can be called, which returns a list of tuples with the shell, contracted function index and the current normalization.
[45]:
pvdz.normalization()
[45]:
[('s', 0, 1.0013033713220225),
('s', 1, 0.23915929699104757),
('s', 2, 1.0),
('p', 0, 0.40825721905456636),
('p', 1, 1.0),
('d', 0, 1.0)]
To normalize the contracted functions simply call the normalize method
[46]:
pvdz.normalize()
to verify we can call the check the normalization again
[47]:
pvdz.normalization()
[47]:
[('s', 0, 0.99999999999999978),
('s', 1, 1.0),
('s', 2, 1.0),
('p', 0, 1.0),
('p', 1, 1.0),
('d', 0, 1.0)]
Uncontracting basis sets¶
The basis sets can be easily uncontract by using the uncontract method. By default the basis set is uncontracted in-place but the copy=True can be specified to obtain an uncotracted copy of the basis set without altering the original.
[48]:
upvdz = pvdz.uncontract(copy=True)
print(upvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Uncontracted:
1 0.0589000000 1.00000000
2 0.1811000000 1.00000000
3 1.1590000000 1.00000000
4 3.1960000000 1.00000000
5 9.1690000000 1.00000000
6 28.4300000000 1.00000000
7 100.5000000000 1.00000000
8 441.2000000000 1.00000000
9 2940.0000000000 1.00000000
================p shell=================
Uncontracted:
1 0.0601800000 1.00000000
2 0.1951000000 1.00000000
3 0.7110000000 1.00000000
4 3.6190000000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
Shell overlap¶
To calculate the overlap matrix between the functions in a given shell you can use the shell_overlap method
[49]:
pvdz.shell_overlap('s')
[49]:
array([[ 1. , -0.20056477, 0.17519428],
[-0.20056477, 1. , 0.74780722],
[ 0.17519428, 0.74780722, 1. ]])
Adding basis sets¶
As an example diffuse functions will be added to the existing BasisSet object with cc-pVDZ basis producing the aug-cc-pVDZ basis. The agumented functions are first parsed from a string to a BasisSet object
[50]:
augstr = '''! aug-cc-pVDZ
basis={
s,Be,1.790000E-02;
c,1.1,1.000000E+00;
p,Be,1.110000E-02;
c,1.1,1.000000E+00;
d,Be,7.220000E-02;
c,1.1,1.000000E+00;
}'''
[51]:
aug = BasisSet.from_str(augstr, fmt='molpro', name='aug functions')
[52]:
print(aug)
Name = aug functions
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Uncontracted:
1 0.0179000000 1.00000000
================p shell=================
Uncontracted:
1 0.0111000000 1.00000000
================d shell=================
Uncontracted:
1 0.0722000000 1.00000000
Addition of two BasisSet object can be done simply by using the + operator. The functions from the second argument are then added to the first argument. The order of the arguments is important since remaining attributes (name, element, family) are copied from the first argument. In the example below the resulting apvdz object retained the name and element attributes from the first argument namely pvdz object. If the addition was done in reverse order (aug + pvdz) the
name of the result would be aug functions.
[53]:
apvdz = pvdz + aug
print(apvdz)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 0.1811000000 0.01257881 1.08532618
2 1.1590000000 0.29488189 -0.27285136
3 3.1960000000 0.45117507 -0.24685753
4 9.1690000000 0.26952641 -0.10894833
5 28.4300000000 0.09992790 -0.03949377
6 100.5000000000 0.02658868 -0.00987855
7 441.2000000000 0.00523259 -0.00197530
8 2940.0000000000 0.00067956 -0.00025151
Uncontracted:
9 0.0589000000 1.00000000
10 0.0179000000 1.00000000
================p shell=================
Contracted:
1 0.1951000000 0.80359641
2 0.7110000000 0.26506765
3 3.6190000000 0.04556068
Uncontracted:
4 0.0601800000 1.00000000
5 0.0111000000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
2 0.0722000000 1.00000000
Serialization¶
Currenly there are two methods supported for serializing BasisSet objects: JSON and pickle.
The default is chosen to be JSON since it provides more flexibility and is human readable.
JSON serialization¶
To serialize a BasisSet to json there is a to_json method
[54]:
jsonstr = apvdz.to_json(indent=4)
print(jsonstr)
{
"name": "cc-pvdz",
"element": "Be",
"family": null,
"kind": null,
"functions": {
"s": {
"e": {
"data": [
0.0589,
0.1811,
1.159,
3.196,
9.169,
28.43,
100.5,
441.2,
2940.0,
0.0179
],
"dtype": "float64"
},
"cf": [
{
"data": [
[
1,
0.01257880524232446
],
[
2,
0.29488189227565326
],
[
3,
0.45117507141868446
],
[
4,
0.26952641069876787
],
[
5,
0.0999278996262612
],
[
6,
0.026588678182035797
],
[
7,
0.005232591105808443
],
[
8,
0.000679557286468629
]
],
"dtype": "CFDTYPE"
},
{
"data": [
[
1,
1.08532617991957
],
[
2,
-0.2728513619301272
],
[
3,
-0.2468575333779799
],
[
4,
-0.10894833112479618
],
[
5,
-0.039493770032738615
],
[
6,
-0.009878554573271215
],
[
7,
-0.001975301949447318
],
[
8,
-0.00025151360225882
]
],
"dtype": "CFDTYPE"
},
{
"data": [
[
0,
1.0
]
],
"dtype": "CFDTYPE"
},
{
"data": [
[
9,
1.0
]
],
"dtype": "CFDTYPE"
}
]
},
"p": {
"e": {
"data": [
0.06018,
0.1951,
0.711,
3.619,
0.0111
],
"dtype": "float64"
},
"cf": [
{
"data": [
[
1,
0.8035964108391421
],
[
2,
0.2650676513400732
],
[
3,
0.04556067899601967
]
],
"dtype": "CFDTYPE"
},
{
"data": [
[
0,
1.0
]
],
"dtype": "CFDTYPE"
},
{
"data": [
[
4,
1.0
]
],
"dtype": "CFDTYPE"
}
]
},
"d": {
"e": {
"data": [
0.238,
0.0722
],
"dtype": "float64"
},
"cf": [
{
"data": [
[
0,
1.0
]
],
"dtype": "CFDTYPE"
},
{
"data": [
[
1,
1.0
]
],
"dtype": "CFDTYPE"
}
]
}
},
"info": null
}
BasisSet can also be created from a JSON string with the from_json method
[55]:
bsfromjson = BasisSet.from_json(jsonstr)
print(bsfromjson)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 0.1811000000 0.01257881 1.08532618
2 1.1590000000 0.29488189 -0.27285136
3 3.1960000000 0.45117507 -0.24685753
4 9.1690000000 0.26952641 -0.10894833
5 28.4300000000 0.09992790 -0.03949377
6 100.5000000000 0.02658868 -0.00987855
7 441.2000000000 0.00523259 -0.00197530
8 2940.0000000000 0.00067956 -0.00025151
Uncontracted:
9 0.0589000000 1.00000000
10 0.0179000000 1.00000000
================p shell=================
Contracted:
1 0.1951000000 0.80359641
2 0.7110000000 0.26506765
3 3.6190000000 0.04556068
Uncontracted:
4 0.0601800000 1.00000000
5 0.0111000000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
2 0.0722000000 1.00000000
pickle serialization¶
Analogously to JSON, to serialize to the BasisSet to pickle there is a to_pickle method which accepts a file anem argument and writes a pickle file to disk.
[56]:
apvdz.to_pickle('aug-cc-pvdz.bas')
The pickle can be read back into the BasisSet object by read_pickle method
[60]:
bsfrompickle = BasisSet.from_pickle('aug-cc-pvdz.bas')
print(bsfrompickle)
Name = cc-pvdz
Element = Be
Family = None
Kind = None
Functions:
================s shell=================
Contracted:
1 0.1811000000 0.01257881 1.08532618
2 1.1590000000 0.29488189 -0.27285136
3 3.1960000000 0.45117507 -0.24685753
4 9.1690000000 0.26952641 -0.10894833
5 28.4300000000 0.09992790 -0.03949377
6 100.5000000000 0.02658868 -0.00987855
7 441.2000000000 0.00523259 -0.00197530
8 2940.0000000000 0.00067956 -0.00025151
Uncontracted:
9 0.0589000000 1.00000000
10 0.0179000000 1.00000000
================p shell=================
Contracted:
1 0.1951000000 0.80359641
2 0.7110000000 0.26506765
3 3.6190000000 0.04556068
Uncontracted:
4 0.0601800000 1.00000000
5 0.0111000000 1.00000000
================d shell=================
Uncontracted:
1 0.2380000000 1.00000000
2 0.0722000000 1.00000000
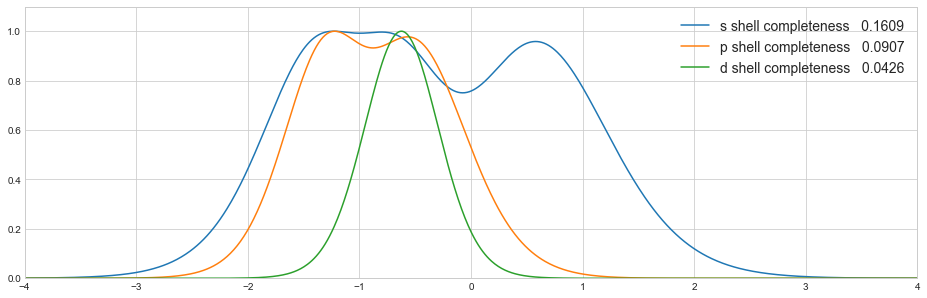
Completeness profiles¶
To visually inspect the quality of the basis set, completeness profiles can be calculated [Chong 1995, Lehtola 2014]. The completeness profile calculation is also implemented in the kruununhaka basis set tool kit.
[63]:
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
%matplotlib inline
To specify the range of scanning exponents for the basis set we’ll use the grid of equidistant points in the \(\log\) space
[64]:
zetas = np.logspace(-10, 10, num=2000, endpoint=True, base=10.0)
The completeness_profile method calculates the profile and returns a numpy array with profile values per shell stored in columns. For convenience we’ll convert the numpy array to a DataFrame
[65]:
cp = pvdz.completeness_profile(zetas)
df = pd.DataFrame(cp, columns=pvdz.functions.keys())
Now we can plot the profiles for each shell together
[66]:
sns.set_style('whitegrid')
plt.figure(figsize=(16, 5))
for shell in df.columns:
c = df[shell].sum()/df[shell].size
plt.plot(np.log10(zetas), df[shell], label='{} shell completeness {:8.4f}'.format(shell, c))
plt.legend(loc='best', frameon=False, fontsize='14')
plt.xlim(-4, 4)
plt.ylim(0.0, 1.1)
plt.show()
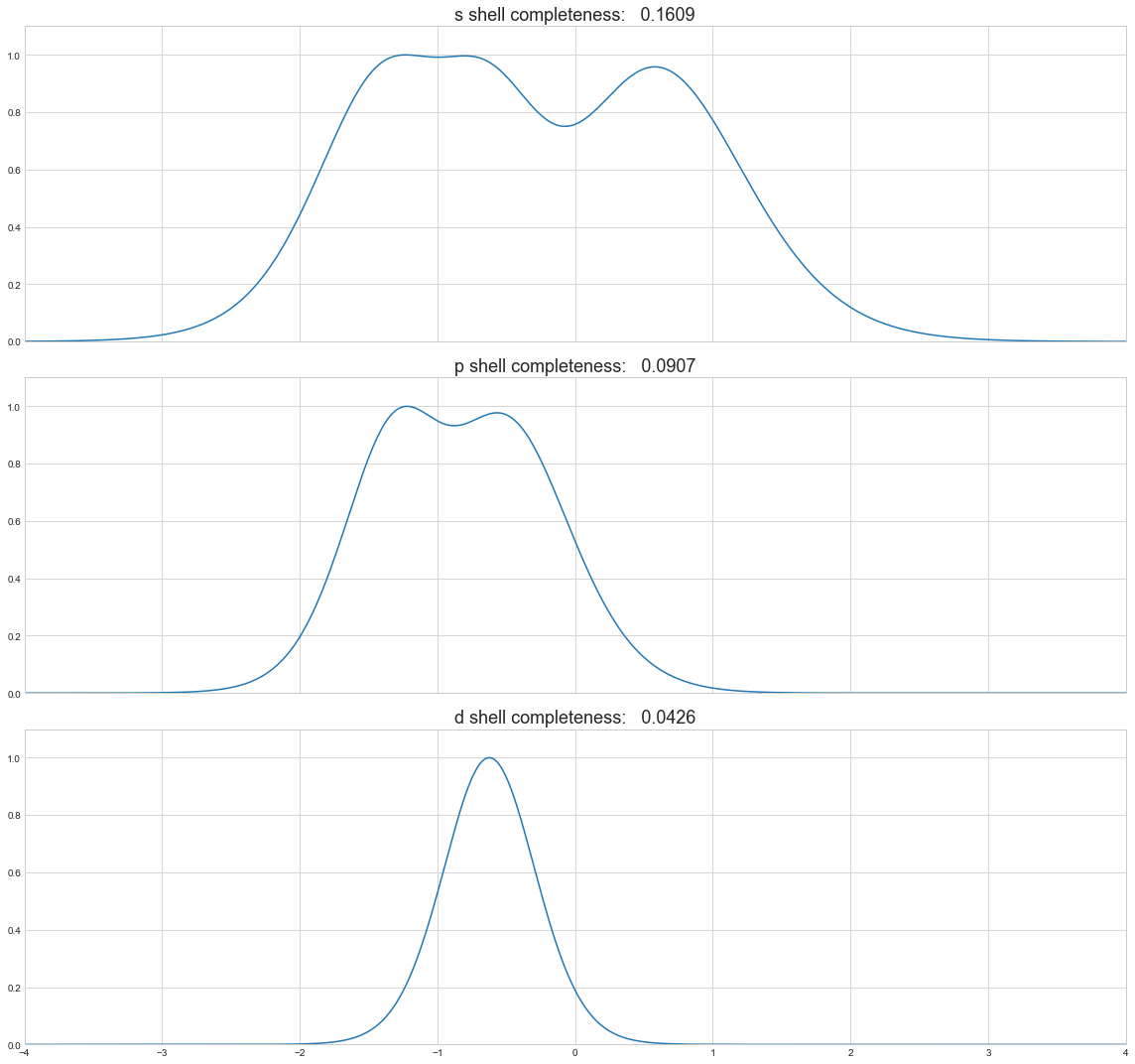
or separately
[67]:
f, axes = plt.subplots(df.shape[1], sharex=True, figsize=(16, 5*df.shape[1]))
for axis, shell in zip(axes, df.columns):
axis.plot(np.log10(zetas), df[shell])
axis.set_title('{} shell completeness: {:8.4f}'.format(shell, df[shell].sum()/df[shell].size), fontsize=18)
axis.set_ylim(0.0, 1.1)
plt.xlim(-4, 4)
plt.tight_layout()
[68]:
%version_information chemtools, mendeleev, scipy, numpy, matplotlib, seaborn
[68]:
| Software | Version |
|---|---|
| Python | 3.6.3 64bit [GCC 7.2.0] |
| IPython | 6.2.1 |
| OS | Linux 4.9.0 4 amd64 x86_64 with debian 9.1 |
| chemtools | 0.8.4 |
| mendeleev | 0.4.0 |
| scipy | 1.0.0 |
| numpy | 1.13.3 |
| matplotlib | 2.1.0 |
| seaborn | 0.8.1 |
| Mon Nov 27 14:11:32 2017 CET | |